Luz e Cor
(* Preparado por C.A. Bertulani para o projeto de Ensino de Física a Distância)
Conceitos Básicos
O estudo de luz e cor deve ser iniciado pela Física elementar, uma vez que a luz é uma onda eletromagnética. | Sendo assim, da Física vem que, todas as ondas eletromagnéticas se propagam no vácuo com a mesma velocidade c com o valor de 3x108 m/s (velocidade da luz). Em decorrência deste fato, e sabendo-se a freqüência de de uma onda eletromagnética (f), no vácuo, pode-se determinar o comprimento de onda (l) desta radiação, através da seguinte equação: l = c/f. |
 |
| O espectro de luz visível, pode então assumir diversas cores (desde o violeta até o vermelho), em função do comprimento de onda, como exposto na tabela ao lado. | Cor l Violeta 380-440 mm Azul 440-490 mm Verde 490-565 mm Amarelo 565-590 mm Laranja 590-630 mm Vermelho 630-780 mm |
| Desta forma, vai-se discutir agora dois fenômenos da Ótica Geométrica: a refelexão e a refração. Para tal, supõe-se que haja um plano, ao qual incide um raio luminoso e que parte deste raio seja refletido por este plano e parte seja refratado. Define-se como ângulo de incidência como sendo o ângulo formado pelo raio e a normal a este plano, ângulo de reflexão entre a normal do plano e raio refletido e ângulo de refração como sendo entre a normal e o raio refratado. |   |
 | Um experimento do conhecimento de todos é que quando a luz branca incide em um prisma, há a decomposição desta nas cores do arco-íris. |
Processo de Formação de Cores
Aproveitando-se então a conclusão de Newton, pode-se então definir que as fontes luminosas brancas possuem todos os comprimentos de onda. Em conseqüência, uma fonte luminosa colorida tem um comprimento de onda dominante que define a sua matiz. |  |
 | As fontes luminosas não são somente caracterizadas pela matiz (hue) que é a presença de um comprimento de onda dominante, também pode-se definir a intensidade ou brilho (brightness) - amplitude do comprimento de onda, e a saturação que é a concentração em torno do comprimento de onda dominante. |

 | O processo de formação de cores por pigmentação, baseia-se na descrição da palheta do pintor, uma vez que a luz ao atingir a camada de pigmentos sofre processos de reflexão, absorção e transmissão (fenômeno conhecido como espalhamento) produzindo assim a(s) cor(es) desejada(s). Esta técnica, como não poderia deixar de ser, é muito utilizada na pintura de quadros. |
| Um outro processo de formação de cores, é o chamado processo aditivo, um exemplo deste processo pode ser visto ao lado, onde duas fontes luminosas de cores diferentes são projetadas em duas regiões. Na área de interseção há a formação de uma nova cor, uma vez que, o olho não consegue distinguir componentes. O processo aditivo é usado, largamente nas televisões comerciais. |  |
 | Um outro processo de formação de cores é o subtrativo que é o processo utilizado em slides. Este processo baseia-se no uso de filtros ou corantes que tem por objetivo filtrar determinados comprimento de onda. Exemplificando, ao se emitir uma luz branca (que possui todos os comprimentos de onda) sobre um filtro verde, este filtra todos os comprimentos de onda deixando só "passar" o comprimento de onda relativa a cor verde, produzindo assim o verde. Na utilização de corantes o processo é o mesmo só que são usados pigmentos que absorvem e refletem alguns comprimentos de onda. |
Percepção humana
Como já foi mencionado anteriormente no processo aditivo de formação de cor, o olho humano não consegue diferenciar componentes e sim a cor resultante; diferentemente do ouvido que consegue distinguir, por exemplo, dois instrumentos diferentes tocados simultaneamente. Desta forma, seria então, interessante saber algo mais sobre o olho humano, responsável pela visão. Os raios luminosos incidem na córnea sendo então refratados. A seguir estes incidem sobre a lente que tem por objetivo projetá-los na retina. Na retina encontram-se dois tipos de fotoreceptores os cones e os bastonetes, que convertem a intensidade e a cor da luz recebida em impulsos nervosos. Estes impulsos são enviados ao cérebro através do nervo ótico e então tem-se a percepção de uma imagem.
 | Os fotoreceptores do olho humano apresentam características totalmente diferentes. Existem na verdade três tipos de cones que respondem a espectro de cores distintos (vermelho, verde e azul), como mostrado ao lado. Sendo assim, diz-se que o sistema visual humano distingue as cores pelo processo da tricromacia. Nota-se que a eficiência do cone que responde a cor azul possui uma eficiência bem menor do que os outros dois tipos de cones. |
Os bastonetes por sua vez, embora sejam maioria absoluta, só conseguem captar a luminosidade da cor, ou seja, só respondem a um espectro e desta forma não diferenciam cores. |  |

O segundo aspecto é o que se denomina de Efeito da Banda de Mach. Analisando-se os tons de cinza da figura a seguir, da cor mais escura para a mais clara, tem-se a impressão que existem pequenas discontinuidades na interface entre as cores (aumento da luminosidade - faixa constante - diminuição da luminosidade).

| O último aspecto a ser abordado é o que se chama de Contraste Simultâneo. Analisando-se a figura ao lado, tem-se a impressão que o quadrado interno da esquerda é mais claro, embora possuam a mesma cor. Este fenômeno pode ser explicado a partir da luminosidade das áreas envolventes, ou seja, quando se tem uma área externa mais escura o quadrado interno parece ser mais claro. |  |
 | Uma vez vistos os aspectos principais do sistema visual humano, resta saber como se dá a percepção de uma cor? Matematicamente falando, deve-se compor em uma integral as componentes vermelha, verde e azul, para obter-se a cor desejada. Este pode ser o processo utlizado por um scanner, mas não pelo olho humano. |
| Restringindo-se o problema de reprodução de cores em Computação Gráfica, há necessidade de uma "combinação linear" das cores básicas para então formar as cores desejadas. A este processo dá-se o nome de metamerismo, ou seja, quando se tem a mesma sensação de cor. |  |
Diagrama de Cromaticidade
 | A Comission Internationale de l'Éclairge (CIE), propôs um método para representação perceptual de cores, utilizando as cores básicas vermelho (Red), verde (Green) e azul (Blue), daqui para frente sendo denominado de RGB. Como já foi visto anteriormente, o olho humano não consegue perceber componentes, desta forma o que se fez foi projetar uma luz em um detreminado anteparo e regulando-se a intensidade das cores RGB tentar produzir a mesma sensação de cor (metamerismo). |
Entretanto, com o sistema proposto anteriormente, não se consegue representar todas as cores visíveis. A solução para contornar este problema, foi de utilizar o artifício da subtração, ou seja, faz-se uma das componentes RGB interagir com a cor desejada, produzindo então uma nova cor procurando com as outras duas restantes conseguir o metamerismo. |  |
 | De acordo com o artifício de subtração utilizado, pode-se montar funções auxiliares, como mostrado ao lado, de modo a formarem as cores espectrais. Deve-se somente frisar que estas funções mostradas não são as distribuições espectrais, e sim funções que se combinadas reproduzem as cores espectrais, como por exemplo a cor C(l). |
 | De forma a não utilizar valores negativos, o CIE, em 1931, definiu padrões primários - X, Ye Z, para substituir as cores RGB, para representar o espectro de cor, como por exemplo apresentado para a cor C(l). Estes padrões não correspondem a estímulos reais de cor, ou seja, não são cores visíveis. Um outro detalhe importante, é que o padrão Y foi escolhido, de forma a ser semelhante à curva de sensibilidade do olho humano (luminância). |
Como já foi mencionado, as cores do sistema XYZ não são realizáveis fisicamente. Sendo assim, pode-se obter as grandezas colorimétricas desse sistema a partir do sistema CIE-RGB, a partir das seguintes hipóteses:
|  |
 | A forma do sólido de cor CIE XYZ (contem todas as cores visíveis) pode ser visto ao lado. Basicamente, é de forma cônica, com o vértice na origem. É apresentado também o plano de crominância ou o plano de Maxwell (X + Y + Z = 1), que tem importância para se obter uma representação paramétrica do espaço de cromaticidade. Pode-se destacar também o triângulo formado pela interseção deste plano com os eixos do espaço de cor XYZ que é chamado triângulo de Maxwell. Analisando-se a figura ao lado, pode-se concluir que as cores visíveis se encontram no primeiro octante do espaço de cor. |
Nota-se que x+y+z = 1, uma vez que x, y e z estão no plano X+Y+Z =1.
 | Sendo assim, retirando o brilho ou a luminosidade da definição da cor em CIE XYZ, e utilizando as coordenadas de cromaticidade x e y, obtem-se o Diagrama de Cromaticidade do CIE. O interior e o contorno deste diagrama com forma de ferradura representam todas as cores visíveis. Todas as cores puras do espectro estão localizadas na região curva do contorno, enquanto que a linha reta deste contorno é chamada de Linha Púrpura ou Linha Magenta, uma vez que ao longo desta linha se encontram as cores púrpuras e magentas saturadas. Estas cores não podem ser definidas por um comprimento de onda dominante e desta forma são denominadas não-espectrais. Destaca-se ainda neste diagrama a luz branca padrão que é definida em um ponto próximo de x = y = z = 1/3. |
Utilizando-se o Diagrama de Cromaticidade do CIE, pode-se visualizar com mais facilidade conceitos como saturação de uma cor e cores complementares. Na parte superior da figura ao lado pode-se dizer que a saturação da cor C1 é definida como sendo a / (a+b). Na parte inferior verifica-se que C é complementar a C pois são cores que quando combinadas produzem a luz branca. Exemplos de cores complementares são: o ciano - vermelho, magenta - verde e amarelo - azul. Este diagrama pode ser útil na visualização de gamutes de monitores e impressoras, e serão vistos adiante no item sobre sistemas de cores utilizados nos dispositivos. |  |
Projeto: Ensino de Física a distância
Desenvolvido por: Carlos Bertulani
O debate sobre o uso consciente dos recursos naturais e uma relação harmônica entre progresso e meio ambiente vem ocupando cada vez mais espaço nas agendas dos líderes mundiais. Com o intuito de avaliar as ações efetivas que vêm sendo implantadas nas principais cidades do mundo, a Siemens patrocinou um estudo realizado pela Economist Intelligence Unit (EIU). O Índice de Cidades Verdes compara as performances em políticas ambientais e proteção climática, avaliando as cidades em oito categorias: energia e CO2, prédios, transporte, lixo, água, saneamento, qualidade do ar e governança ambiental.
Esse estudo engloba Estados Unidos e Canadá, América Latina, Europa, Alemanha e Ásia. Através de uma ferramenta online é possível consultar o desempenho de diversas cidades do mundo. Para isso, basta acessar o site e clicar no continente onde está localizada a cidade que se deseja pesquisar. O resultado geral é apresentado em um ranking dividido em cinco classificações: “bem abaixo da média”, “abaixo da média”, “na média”, “acima da média” e “bem acima da média”.
A análise da América Latina envolveu 17 cidades de oito países, incluindo o Brasil, e pode ser lida em detalhes neste PDF. Belo Horizonte, Bogotá, Brasília, Buenos Aires, Cidade do México, Curitiba, Guadalajara, Lima, Medellín, Monterrey, Montevidéu, Porto Alegre, Puebla, Quito, Rio de Janeiro, Santiago e São Paulo foram analisadas nas oito categorias previstas pelo estudo. Curitiba, no Paraná, foi a cidade com o melhor resultado geral. Entre as cidades brasileiras, apenas Porto Alegre obteve um desempenho “na média”. Belo Horizonte, Brasília, Rio de Janeiro e São Paulo ficaram “acima da média” e Curitiba foi a única “bem acima da média” entre todas as cidades analisadas na América Latina.
Esse estudo engloba Estados Unidos e Canadá, América Latina, Europa, Alemanha e Ásia. Através de uma ferramenta online é possível consultar o desempenho de diversas cidades do mundo. Para isso, basta acessar o site e clicar no continente onde está localizada a cidade que se deseja pesquisar. O resultado geral é apresentado em um ranking dividido em cinco classificações: “bem abaixo da média”, “abaixo da média”, “na média”, “acima da média” e “bem acima da média”.
A análise da América Latina envolveu 17 cidades de oito países, incluindo o Brasil, e pode ser lida em detalhes neste PDF. Belo Horizonte, Bogotá, Brasília, Buenos Aires, Cidade do México, Curitiba, Guadalajara, Lima, Medellín, Monterrey, Montevidéu, Porto Alegre, Puebla, Quito, Rio de Janeiro, Santiago e São Paulo foram analisadas nas oito categorias previstas pelo estudo. Curitiba, no Paraná, foi a cidade com o melhor resultado geral. Entre as cidades brasileiras, apenas Porto Alegre obteve um desempenho “na média”. Belo Horizonte, Brasília, Rio de Janeiro e São Paulo ficaram “acima da média” e Curitiba foi a única “bem acima da média” entre todas as cidades analisadas na América Latina.

Rio de Janeiro. Foto: Denise Mayumi
Os resultados da pesquisa são de grande valor, uma vez que a classificação em cada categoria de análise é feita a partir de uma comparação entre as realidades de cada uma dessas cidades, e não de um ideal abstrato. Nesse sentido, o estudo possibilita não apenas uma melhor compreensão dos desafios dessas cidades em meio ambiente como também promove um intercâmbio de ideias sobre como reduzir o impacto ambiental. O vídeo abaixo, por exemplo, mostra o funcionamento da rede de transportes de Curitiba, um projeto de tráfego bem articulado e funcional que poderia facilmente servir de inspiração para outras cidades brasileiras.
A velocidade da luz no vácuo, simbolizada pela letra c, é definida como 299 792 458 metros por segundo[1]. O símbolo c origina-se do Latim celeritas, velocidade ou rapidez[2]. A velocidade da luz em um meio material transparente, tal como o vidro ou o ar, é menor que c, sendo a fração função do índice de refração do meio.
A unidade fundamental do SI para comprimentos, o metro, é definida desde 21 de outubro de 1983 como a distância que a luz viaja no vácuo em 1/299 792 458 do segundo; qualquer aumento na precisão da medida de velocidade da luz iria certamente refinar a definição do metro, mas não alterar o valor numérico do c.
Índice[esconder] |
[editar] Visão geral
De acordo com a moderna física teórica, toda radiação eletromagnética, incluindo a luz visível, se propaga (ou move) no vácuo a uma velocidade constante, chamada de velocidade da luz, que é uma constante da Física, representada por c. É também a velocidade de propagação da atração gravitacional, na teoria geral da relatividade.Uma consequência das equações de Maxwell, referentes ao eletromagnetismo, é que a velocidade c da radiação eletromagnética não depende da velocidade do objeto que emite a radiação, de modo que a velocidade da luz emitida por uma fonte em alta velocidade é a mesma que a de outra fonte estacionária, embora a frequência (que define a cor) e a energia sejam diferentes, por causa do efeito Doppler relativístico. Todos os observadores que medem a velocidade da luz no vácuo chegam ao mesmo resultado. Por isso c é uma constante física fundamental e a constância da velocidade da luz no vácuo é um dos fundamentos da teoria da relatividade especial. Distâncias astronômicas são frequentemente medidas em anos-luz, que é a distância que a luz percorre em um ano solar, aproximadamente 9,46×1012 quilômetros.
[editar] Interação com materiais transparentes
Passando por materiais transparentes, a velocidade da luz é reduzida a uma fração de c , sendo esse seu índice de refração, uma característica do material. No ar, a velocidade é pouco menor que c, enquanto materiais mais densos como água ou vidro podem reduzir a velocidade da luz para 70 a 60% de c. Fibras ópticas, muito utilizadas em telecomunicações, normalmente reduzem 30% da velocidade. Essa redução também é responsável pelo fenômeno da refração, quando a luz passa de um material para outro.Como a velocidade depende do índice de refração, e este depende da frequência da luz, tem-se que a luz em diferentes frequências viaja a diferentes velocidades no mesmo material. Isto pode causar distorções das ondas eletromagnéticas chamadas de dispersão. Deve-se notar que ao voltar de um meio físico para o vácuo, a luz reassume a velocidade c sem receber nenhuma energia.
[editar] Desacelerando a luz
Certos materiais especiais, como o condensado de Bose-Einstein, têm um índice de refração altíssimo, reduzindo a velocidade da luz a meros 17 metros por segundo. Em um experimento em 2001, a equipe da cientista Lene Hau conseguiu mesmo pará-la por instantes.[3][editar] História
Desde a antiguidade clássica, vários filósofos especularam sobre a velocidade da luz. Empédocles, Aristóteles e Heron na Grécia e os árabes Avicena e Alhazen deixaram, também, suas opiniões. O indiano , no século XIV, deixou um comentário no Rig Veda (estimados 302 000 m/s).Johannes Kepler, Francis Bacon e René Descartes, na Europa, também citaram o assunto. Galileu Galilei propôs um experimento em 1638, realizado em Florença no ano de 1667, que fracassou. A primeira técnica de medição foi acidentalmente descoberta em 1676 por Ole Romer. Enquanto observava Júpiter e seu satélite Io, notou que havia um atraso, o que o levou a comentar num congresso de astronomia que a velocidade da luz poderia ser muito alta. Suas medições, combinadas com outras de Christiaan Huygens, chegaram a um valor abaixo do valor real mas muito mais alto do que o de qualquer fenômeno conhecido então. Newton, em seu livro Opticks, aceita um valor quase igual ao de Romer.
Foram, no entanto, as observações de James Bradley em 1728 que elucidaram a questão, calculando a velocidade num valor apenas um pouco menor que o aceito atualmente. Léon Foucault, usando a roda de medir a velocidade da luz inventada por Fizeau, publicou uma aproximação melhor, e finalmente, em 1926, Albert Michelson, do observatório de Monte Wilson, publicou um valor preciso.
[editar] Eletromagnetismo
Ao resolver as equações de Maxwell no vácuo e sem fontes de campo é possível obter a velocidade de uma onda eletromagnética. Segue o procedimento:| Esta velocidade é tão próxima da velocidade da luz que parece que temos fortes motivos para concluir que a luz em si (incluindo calor radiante, e outras radiações do tipo) é uma perturbação eletromagnética na forma de ondas propagadas através do campo eletromagnético de acordo com as leis eletromagnéticas. |


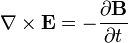








Nenhum comentário:
Postar um comentário